Important Information
You can view this page as a webpage or access this as a regular github repository.
The source of this example can be found here and the output here.
See the top directory of this repository for instructions to set up the NAG Library for Java.
Rosenbrock function: Bound constrained optimization
First order active set bound-constrained nonlinear programming
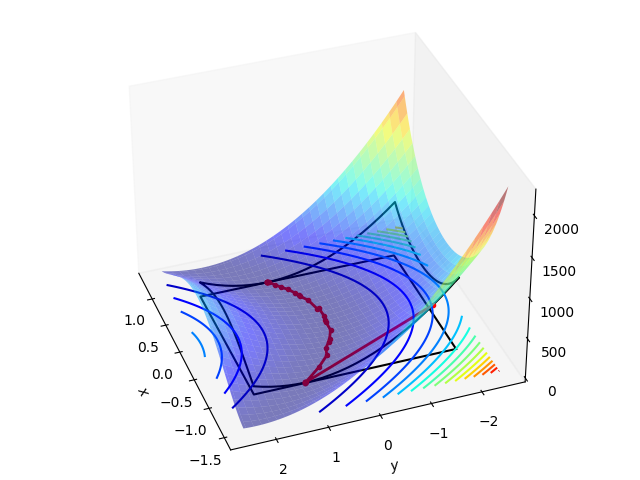
2d Rosenbrock example: This page illustrates the usage of FOAS to solve the bound-constrained 2d Rosenbrock function. There is a plot at the end showing the steps taken by the solver to find the solution point.
Add objective function, gradient and monitoring callback
/**
* The objective's function.
*/
public static class OBJFUN extends E04KF.Abstract_E04KF_OBJFUN {
public void eval() {
this.FX = objfunEval(this.X[0], this.X[1]);
}
}
/**
* The objective's gradient.
*/
public static class OBJGRD extends E04KF.Abstract_E04KF_OBJGRD {
public void eval() {
this.FDX[0] = 2.0 * this.X[0] - 400.0 * this.X[0] * (this.X[1] - Math.pow(this.X[0], 2)) - 2.0;
this.FDX[1] = 200.0 * (this.X[1] - Math.pow(this.X[0], 2));
}
}
/**
* The monitor function.
*/
public static class MONIT extends E04KF.Abstract_E04KF_MONIT {
public void eval() {
steps[0].add(this.X[0]);
steps[1].add(this.X[1]);
steps[2].add(this.RINFO[0]);
}
}
Specify initial guess
double[] x = new double[] { -1.0, -1.5 };
Define the nonlinear objective (add to handle)
E04RA e04ra = new E04RA();
E04RG e04rg = new E04RG();
E04RH e04rh = new E04RH();
E04ZM e04zm = new E04ZM();
E04KF e04kf = new E04KF();
ifail = 0;
e04ra.eval(handle, nvar, ifail);
handle = e04ra.getHANDLE();
ifail = 0;
e04rg.eval(handle, nvar, idxfd, ifail);
Add the box bounds on the variable x to the handle
double[] bl = new double[] { -1.0, -2.0 };
double[] bu = new double[] { 0.8, 2.0 };
ifail = 0;
e04rh.eval(handle, nvar, bl, bu, ifail);
Set some algorithmic options
ifail = 0;
e04zm.eval(handle, "FOAS Print Frequency = 1", ifail);
e04zm.eval(handle, "Print Solution = yes", ifail);
e04zm.eval(handle, "FOAS Monitor Frequency = 1", ifail);
e04zm.eval(handle, "Print Level = 2", ifail);
e04zm.eval(handle, "Monitoring Level = 1", ifail);
Solve the problem
OBJFUN objfun = new OBJFUN();
OBJGRD objgrd = new OBJGRD();
MONIT monit = new MONIT();
double[] rinfo = new double[100];
double[] stats = new double[100];
int[] iuser = new int[0];
double[] ruser = new double[0];
long cpuser = 0;
ifail = 0;
e04kf.eval(handle, objfun, objgrd, monit, nvar, x, rinfo, stats, iuser, ruser, cpuser, ifail);
// Add last step
steps[0].add(x[0]);
steps[1].add(x[1]);
steps[2].add(rinfo[0]);
----------------------------------------------------------
E04KF, First order method for bound-constrained problems
----------------------------------------------------------
Begin of Options
Print File = 6 * d
Print Level = 2 * U
Print Options = Yes * d
Print Solution = All * U
Monitoring File = -1 * d
Monitoring Level = 1 * U
Foas Monitor Frequency = 1 * U
Foas Print Frequency = 1 * U
Infinite Bound Size = 1.00000E+20 * d
Task = Minimize * d
Stats Time = No * d
Time Limit = 1.00000E+06 * d
Verify Derivatives = No * d
Foas Estimate Derivatives = No * d
Foas Finite Diff Interval = 1.05367E-08 * d
Foas Iteration Limit = 10000000 * d
Foas Memory = 11 * d
Foas Progress Tolerance = 1.08158E-12 * d
Foas Rel Stop Tolerance = 1.08158E-12 * d
Foas Restart Factor = 6.00000E+00 * d
Foas Slow Tolerance = 1.01316E-02 * d
Foas Stop Tolerance = 1.00000E-06 * d
Foas Tolerance Norm = Infinity * d
End of Options
Problem Statistics
No of variables 2
free (unconstrained) 0
bounded 2
Objective function Nonlinear
-------------------------------------------------------------------------------
iters | objective | optim | dir
-------------------------------------------------------------------------------
0 6.29000E+02 5.00E+02 3.50E+00
1 6.29000E+02 5.00E+02 3.50E+00
2 4.00000E+00 0.00E+00 1.80E+00
3 4.00000E+00 0.00E+00 1.80E+00
4 3.99156E+00 2.80E+00 2.80E+00
5 3.99156E+00 2.80E+00 2.80E+00
6 3.98433E+00 1.44E+00 1.44E+00
7 3.97076E+00 5.76E+00 1.79E+00
8 3.41157E+00 1.66E+01 1.60E+00
9 3.15876E+00 2.07E+01 1.65E+00
10 2.34744E+00 2.55E+00 2.29E+00
11 2.06122E+00 5.09E+00 1.83E+00
12 1.97065E+00 6.49E+00 1.88E+00
13 1.77751E+00 9.58E+00 1.99E+00
14 1.19453E+00 2.20E+00 8.93E-01
15 1.12429E+00 2.33E+00 2.01E+00
16 1.01998E+00 5.04E+00 2.02E+00
17 8.94996E-01 8.97E+00 2.02E+00
18 7.06184E-01 1.32E+00 1.10E+00
19 5.06340E-01 5.11E+00 1.91E+00
-------------------------------------------------------------------------------
iters | objective | optim | dir
-------------------------------------------------------------------------------
20 3.21115E-01 1.03E+00 3.67E-01
21 2.99551E-01 9.31E-01 9.31E-01
22 2.51003E-01 2.68E+00 1.75E+00
23 2.14196E-01 4.82E+00 1.66E+00
24 1.15236E-01 1.17E+00 3.70E-01
25 8.06733E-02 1.98E+00 1.73E+00
26 6.60815E-02 4.33E+00 1.79E+00
27 5.37636E-02 3.33E+00 1.80E+00
28 4.02960E-02 3.44E-01 3.44E-01
29 4.02960E-02 3.44E-01 3.44E-01
30 4.00937E-02 1.94E-01 1.94E-01
31 4.00937E-02 1.94E-01 1.94E-01
32 4.00000E-02 0.00E+00 0.00E+00
-------------------------------------------------------------------------------
Status: converged, an optimal solution was found
-------------------------------------------------------------------------------
Value of the objective 4.00000E-02
Norm of inactive gradient 0.00000E+00
Norm of projected direction 0.00000E+00
Iterations 32
Function evaluations 75
FD func. evaluations 0
Gradient evaluations 36
NPG function calls 18
NPG gradient calls 3
CG function calls 9
CG gradient calls 5
LCG function calls 48
LCG gradient calls 28
-------------------------------------------------------------------------------
Primal variables:
idx Lower bound Value Upper bound
1 -1.00000E+00 8.00000E-01 8.00000E-01
2 -2.00000E+00 6.40000E-01 2.00000E+00
Box bounds dual variables:
idx Lower bound Value Upper bound Value
1 -1.00000E+00 0.00000E+00 8.00000E-01 4.00000E-01
2 -2.00000E+00 0.00000E+00 2.00000E+00 0.00000E+00
Retrieve Lagrange multipliers
double[] mult = new double[2 * nvar];
Arrays.fill(mult, 0.0);
E04RX e04rx = new E04RX();
ifail = 0;
e04rx.eval(handle, "Dual Variables", 1, 2 * nvar, mult, ifail);
double[] mult_t = new double[mult.length / 2];
for (int i = 0; i < mult.length; i += 2) {
mult_t[i / 2] = mult[i] - mult[i + 1];
}
Lagrange multipliers: [ -0.4 0.0 ]
Destroy the handle
E04RZ e04rz = new E04RZ();
e04rz.eval(handle, ifail);
Evaluate the funtion over the domain
double[] x_m = linspace(bl[0] - 0.5, bu[0] + 0.5, 101);
double[] y_m = linspace(bl[1] - 0.5, bu[1] + 0.5, 101);
double[][] z_m = new double[101][101];
for (int i = 0; i < 101; i++) {
for (int j = 0; j < 101; j++) {
z_m[i][j] = objfunEval(x_m[i], y_m[i]);
}
}
int inform = 1;
int nb = 25;
double[] x_box = linspace(bl[0], bu[0], nb);
double[] y_box = linspace(bl[1], bu[1], nb);
double[][] box = new double[2][100];
for (int i = 0; i < nb; i++) {
box[0][i] = x_box[i];
box[0][nb + i] = bu[0];
box[0][nb * 2 + i] = x_box[nb - 1 - i];
box[0][nb * 3 + i] = bl[0];
box[1][i] = bl[1];
box[1][nb + i] = y_box[i];
box[1][nb * 2 + i] = bu[1];
box[1][nb * 3 + i] = y_box[nb - 1 - i];
}
double[] z_box = new double[box[0].length];
for (int i = 0; i < z_box.length; i++) {
z_box[i] = objfunEval(box[0][i], box[1][i]);
}
double[][] X = new double[x_m.length][x_m.length];
double[][] Y = new double[y_m.length][y_m.length];
for (int i = 0; i < X.length; i++) {
Arrays.fill(X[i], x_m[i]);
Arrays.fill(Y[i], y_m[i]);
}
Plot function and steps taken