Important Information
This file has a lot of Latex and GitHub currently cannot render it on Markdown files. You can read all the math clearly as a webpage or access this as a regular github repository.
The source of this example can be found here and the output here.
See the top directory of this repository for instructions to set up the NAG Library for Java.
Fast Implied Volatilities using the NAG Library
The Black-Scholes formula for the price of a European call option is
\[P = S_0\Phi\left(\frac{\ln\left(\frac{S_0}{K}\right)+\left[r+\frac{\sigma^2}{2}\right]T}{\sigma\sqrt{T}}\right) - Ke^{-rT}\Phi\left(\frac{\ln\left(\frac{S_0}{K}\right)+\left[r-\frac{\sigma^2}{2}\right]T}{\sigma\sqrt{T}}\right),\]where \(T\) is the time to maturity, \(S_0\) is the spot price of the underlying asset, \(K\) is the strike price, \(r\) is the interest rate and \(\sigma\) is the volatility. A similar formula applies for European put options.
An important problem in finance is to compute the implied volatility, \(σ\), given values for \(T\), \(K\), \(S_0\), \(r\) and \(P\). An explicit formula for \(\sigma\) is not available. Furthermore, \(\sigma\) cannot be directly measured from financial data. Instead, it must be computed using a numerical approximation. Typically, multiple values of the input data are provided, so the Black-Scholes formula must be solved many times.
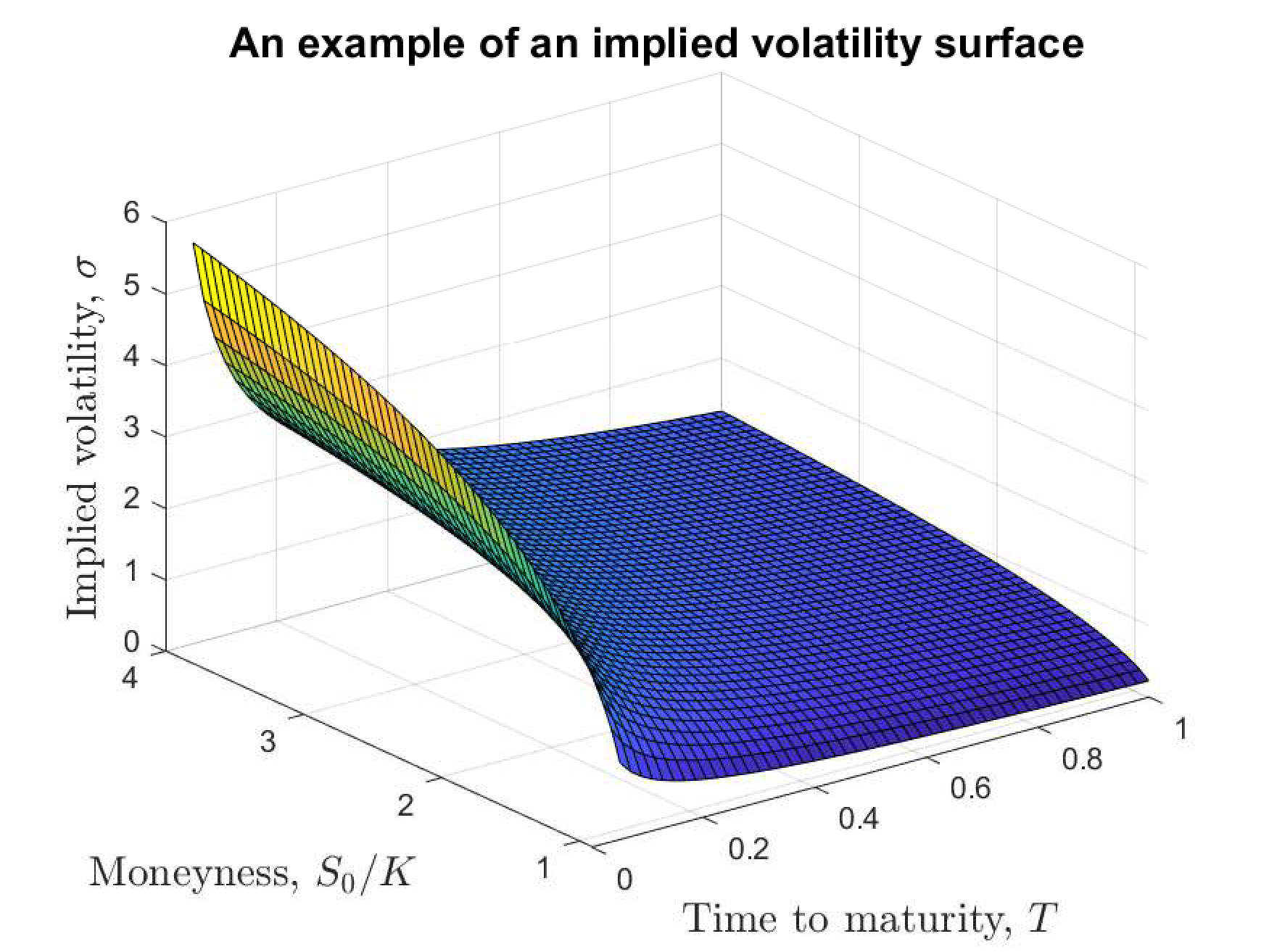
As shown in the figure below, the volatility surface (a three-dimensional plot of how the volatility varies according to the price and time to maturity) can be highly curved. This makes accurately computing the implied volatility a difficult problem.
Before introducing our new NAG Library routine, let’s demonstrate how one might naively compute implied volatilities using a general purpose root finder.
Let’s generate some input data using a random number generator from the NAG Library:
G05KG g05kg = new G05KG();
G05SQ g05sq = new G05SQ();
int ifail = 0;
int lstate = 17;
int[] state = new int[lstate];
int n = 10000; // This is the number of volatilities we will be computing
double[] p = new double[n];
double[] k = new double[n];
double[] s0 = new double[n];
double[] t = new double[n];
double[] r = new double[n];
g05kg.eval(1, 0, state, lstate, ifail);
g05sq.eval(n, 3.9, 5.8, state, p, ifail);
g05sq.eval(n, 271.5, 272.0, state, k, ifail);
g05sq.eval(n, 259.0, 271.0, state, s0, ifail);
g05sq.eval(n, 0.016, 0.017, state, t, ifail);
g05sq.eval(n, 0.017, 0.018, state, r, ifail);
We have chosen the limits of the various uniform distributions above to ensure the input data takes sensible values.
There are various standard root finding techniques that we could use to compute implied volatilities,
a common example being bisection. The NAG Library routine C05AW, is a general
purpose root finder based on the secant method. It uses a callback, with data passed in via a communication object:
public static class BlackScholes extends C05AW.Abstract_C05AW_F {
public double eval() {
double[] price = new double[1];
int ifail = 1;
S30AA s30aa = new S30AA();
s30aa.eval("C", 1, 1, new double[]{this.getRUSER()[1]}, this.getRUSER()[2], new double[]{this.getRUSER()[3]}, this.getX(), this.getRUSER()[4], 0.0, price, 1, ifail);
ifail = s30aa.getIFAIL();
if (ifail != 0)
price[0] = 0.0;
return price[0] - this.getRUSER()[0];
}
}
C05AW operates on scalars, so we need to call the routine
once for every volatility we want to compute. We will time the computation and count how many errors are caught:
int[] iuser = new int[5];
double[] ruser = new double[5];
int errorcount = 0;
double sigma;
C05AW c05aw = new C05AW();
BlackScholes blackScholes = new BlackScholes();
long tic = System.currentTimeMillis();
for (i = 0; i < n; i++) {
//System.out.println("Info: i = " + i);
ruser[0] = p[i];
ruser[1] = k[i];
ruser[2] = s0[i];
ruser[3] = t[i];
ruser[4] = r[i];
ifail = 1;
c05aw.eval(0.15, 1.0e-14, 0.0, blackScholes, 500, iuser, ruser, ifail);
sigma = c05aw.getX();
ifail = c05aw.getIFAIL();
if ((sigma < 0.0) || (ifail != 0)) {
errorcount++;
}
}
long toc = System.currentTimeMillis();
System.out.println("Using a general purpose root finder:");
System.out.printf(" Time taken: %.5f seconds\n", (toc-tic)/1000.0);
System.out.printf(" There were %d failures\n", errorcount);
Can a bespoke implied volatility routine do better? Our new routine at Mark 27.1 is called S30AC. We call it as follows:
s30ac.eval("C", n, p, k, s0, t, r, sigma_arr, 2, ivalid, ifail);
The return argument ivalid is an array recording any data points for which the volatility could not be computed. The argument mode allows us to select which algorithm to use – more on that in a moment, but
for now we choose mode=2. This selects the algorithm of Jäckel (2015), a very accurate method based
on third order Householder iterations.
Here is the call surrounded by some timing code:
S30AC s30ac = new S30AC();
double[] sigma_arr = new double[n];
int[] ivalid = new int[n];
tic = System.currentTimeMillis();
ifail = 0;
s30ac.eval("C", n, p, k, s0, t, r, sigma_arr, 2, ivalid, ifail);
toc = System.currentTimeMillis();
System.out.println("S30AC with mode = 2 (Jäckel algorithm):");
System.out.printf(" Time taken: %.5f seconds\n", (toc-tic)/1000.0);
System.out.printf(" There were %d failures\n", nonZeroLength(ivalid));
The new routine is several orders of magnitude faster than the root finder, with no failures reported. We could try
tweaking the convergence parameters and iteration limits in C05AW, and we could certainly
improve the way data is passed through the callback, but we are unlikely to match the
performance of S30AC.
Recently NAG embarked upon a collaboration with mathematicians at Queen Mary University of
London, who have been developing an alternative algorithm for computing implied volatilities. The new
algorithm (based on Glau et. al. (2018)) uses Chebyshev interpolation to remove branching and give
increased SIMD performance. We access it by setting mode=1 in the call to S30AC:
tic = System.currentTimeMillis();
ifail = 0;
s30ac.eval("C", n, p, k, s0, t, r, sigma_arr, 1, ivalid, ifail);
toc = System.currentTimeMillis();
System.out.println("S30AC with mode = 1 (Glau algorithm):");
System.out.printf(" Time taken: %.5f seconds\n", (toc-tic)/1000.0);
System.out.printf(" There were %d failures\n", nonZeroLength(ivalid));
Depending on your system, you should find that, for similar accuracy, there is a modest speedup over the Jäckel algorithm. Our numerical experiments have shown that for very small arrays (containing fewer than 100 elements) the Jäckel algorithm actually outperforms that of Glau et.al., but for larger arrays the converse is true. As vector units continue to improve in the future, we expect the performance of the highly vectorizable Glau et.al. approach to improve similarly.
So far, we have been computing implied volatilities with a relative accuracy as close as possible to
double precision. However, in some applications implied volatilities are only required with a few decimal
places of precision. One advantage of the Glau et.al. algorithm is that it can be run in a lower accuracy
mode, aiming only for seven decimal places of accuracy. This is accessed by setting mode=0 in the call
to S30AC. It roughly doubles the speed of the routine:
tic = System.currentTimeMillis();
ifail = 0;
s30ac.eval("C", n, p, k, s0, t, r, sigma_arr, 0, ivalid, ifail);
toc = System.currentTimeMillis();
System.out.println("S30AC with mode = 0 (lower accuracy Glau algorithm):");
System.out.printf(" Time taken: %.5f seconds\n", (toc-tic)/1000.0);
System.out.printf(" There were %d failures\n", nonZeroLength(ivalid));
The charts below summarize the results, using timings collected on an Intel Skylake machine. We can see that the Glau et.al. algorithm outperforms the Jäckel algorithm for large arrays but not for small arrays. Note that the general purpose root finder
is omitted here as it is so much slower S30AC.
In summary, NAG’s new state-of-the art algorithm can be run in three different modes, according to the length of the input arrays and the required accuracy. For more information, and to access the NAG Library, go to: https://www.nag.co.uk/content/nag-library.
References
P. Jäckel (2015). Let’s be rational. Wilmott 2015, 40-53.
K. Glau, P. Herold, D. B. Madan, C. Pötz (2019). The Chebyshev method for the implied volatility. Journal of Computational Finance, 23(3).